最高のコレクション 中2 数学 連立方程式 311532

中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
数学やっていきましょう! 今回は 2つの方程式を組みにした 「連立方程式」を学習します 中2数学で 一番大切と言っても良い 単元ですので 一緒にしっかり やっていきましょう動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
中2 数学 連立方程式
中2 数学 連立方程式-(2) 連立方程式の解き方やそのアイデアを発見することができる。また,問題解決の場面で数量の関 係を整理し,連立方程式をつくることができる。(数学的な見方や考え方) (3) 連立方程式を代入法や加減法を使って解くことができる。(数学的な技能) 連立方程式教えてくださいm(_ _)m 中2の数学です。 タイトルの通り、連立方程式が式の立て方から解き方まで全部わかんないです汗 できればとても基本的な所から、あとは連立方程式の利用(文章題など)くらいまでできるように解説していただければ、光栄です!
中学数学単元別 連立方程式 数学中学校教材問題集 Buyee 日本代购平台 产品购物网站大全 Buyee一站式代购bot Online
連立方程式の利用 <応用問題(1)> 中2数学 今回も連立方程式の利用です。 基本的な問題が解けて、難しい問題へのステップアップとしての問題となります。 連立方程式の利用の基本的な問題が解けない場合は『 連立方程式の利用<基本篇> 』から2年生 2 連立方程式 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 解が(x ,y )=(-1,4)になる連立二元一次方程式を1つつくりなさい。 2 解が(x ,y )=(2,1)になる連立方程式を次のアからオの中からすべて選びなさい。 ア 2x +y =1 イ 3x +4y =10 ウ 2x -3y =7 中2数学 連立方程式発展 連立方程式は得意! という人でも、解き方を知らないと難しい問題もあります。 普通連立方程式といえばx,yを求めるものですが、中には2組の連立方程式からx,yだけでなくa,bも求める問題があります。 またA=B=Cと3つの式を=で
試験問題連立方程式2 試験問題A=B=C型 試験問題まとめ 次の連立方程式を解きなさい. (答案は半角小文字の英字,数字,符号及び不等号で入力し,最終形はxを左辺にして答えなさい.なお,タブキーでも空欄移動ができます.採点の結果 ,間違ってい 中2数学 ブーメラン型四角形(凹四角形)の角度を求める方法 中2数学 「平行線と面積」で覚えておきたい2つのこと 中1数学 一次方程式道のり・速さの文章問題(追いつく系)の解き方 中2数学 19 中2数学「連立方程式の計算」の問題 どこよりも簡単な解き方・求め方 今回は、2つの方程式を組みにした「連立方程式」を学習します 中2数学で一番大切と言っても良い単元ですので、一緒にしっかりやっていきましょう
中2 数学 連立方程式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | 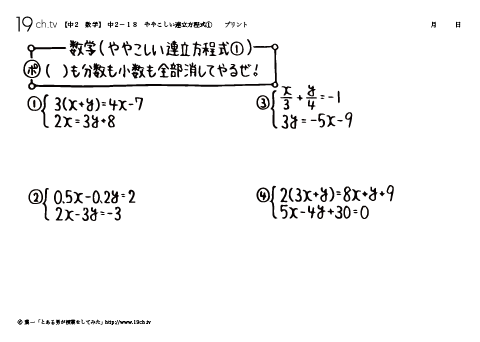 |  |
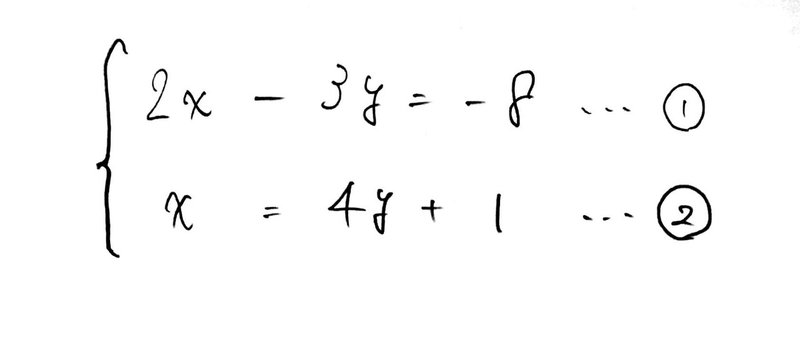 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 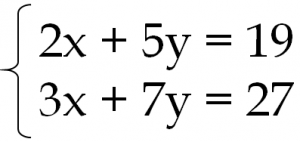 |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「中2 数学 連立方程式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
中学生の諸君。「中2数学」で差がつくポイント、「連立方程式」にはコツがあるぞ。(ビシッ)差がつくのはココだ!(ビシッ)トォォォ~ッ! オール5家庭教師、見参ッ! 加減法、代入法どっちも来い! 文章題も! 勝負の無料サイトだ。3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は? 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説! 池の周りを追いつく速さの問題を解説!←今回の記事
コメント
コメントを投稿